- Autor admin [email protected].
- Public 2023-12-16 19:27.
- Naposledy zmenené 2025-06-01 06:13.

Príklady zlatého rezu možno nájsť všade v klasickej architektúre, umeleckých dielach, prírode a dokonca aj v hudbe. Toto vyjadrenie proporcie, tiež známe ako Divine Ratio, ponúka harmonickú kompozíciu prostredníctvom aplikácie iracionálneho čísla (1,618) v dizajne, či už prirodzenom alebo ľudskom. S najväčšou pravdepodobnosťou si neuvedomujete matematiku, ktorá stojí za krásou Zlatého rezu, pretože produkuje predmety a hudbu, ktoré vás prirodzene potešia bez potreby akéhokoľvek vysvetľovania.
Zlatý pomer v architektúre
Zlatý pomer vytvára takmer dokonalú krásu prírody a umenia. Keď začnete hľadať príklady zlatého pomeru v každodennom živote, možno vás prekvapí množstvo príkladov, ktoré boli použité na vytvorenie mnohých monumentálnych budov a stavieb. Keď sa v architektúre používa zlatý pomer, hovorí sa, že budova je vytvorená pomocou „posvätnej architektúry“. Aplikovaním výpočtu zlatého pomeru na štvorec dokážu architekti a dizajnéri vytvoriť zlatý obdĺžnik, o ktorom sa predpokladá, že má pre ľudské oko najestetickejšie proporcie.
Zlatý obdĺžnik Príklad: Parthenon

Phidias, grécky sochár, používal vo svojej tvorbe zlatý rez, najmä keď začal pracovať s kapelami, ktoré vytesal tesne nad stĺpmi Parthenonu. Je tiež dôležité poznamenať, že číselná hodnota priradená zlatému pomeru, Phi, bola pomenovaná na jeho počesť.
Ak zmeriate rozmery exteriéru Parthenonu, zistíte, že netvorí len zlatý obdĺžnik, ale že medzi stĺpmi je aj veľa zlatých obdĺžnikov. Táto posvätná stavba je krásnym príkladom zlatého pomeru v architektúre.
Príklad zlatého trojuholníka: Veľká pyramída v Gíze
Zlatý pomer, zlatý obdĺžnik a zlatý trojuholník, to všetko možno nájsť v dokonalosti jedného zo siedmich divov sveta, Veľkej pyramídy v Gíze. Ak chcete nájsť zlatý pomer, budete musieť rozdeliť štvorcovú základňu pyramídy na polovicu a nakresliť zvislú čiaru do stredu pyramídy. Keď je toto spojené so šikmou stranou pyramídy, môžete ľahko vidieť, ako tvorí zlatý trojuholník s pomerom 1,618, zlatý pomer.
Ďalšie architektonické príklady
Môžete nájsť veľa príkladov starovekej až modernej sakrálnej architektúry a budov Zlatého rezu.
- Katedrála Chartres - Centre, Francúzsko
- Notre Dame - Paríž, Francúzsko
- Porch of Maidens - Akropola, Atény
- Taj Mahal - Agra, India
- Budova Organizácie Spojených národov - New York City, New York
Zlatý pomer v umeleckých príkladoch
Môžete nájsť veľa príkladov majstrov maliarov, ktorí používali zlatý rez. Tieto diela dokonalosti boli vytvorené použitím pomeru zlatých obdĺžnikov a zlatých trojuholníkov. Umenie vytvorené na základe Zlatého obdĺžnika sa ukazuje ako príjemnejšie pre ľudské oko. Je to jedna zo záhad, ktorá obklopuje tento dokonalý obdĺžnik a zlatý rez.
Zlatý pomer v umení

Príklady umenia so zlatým pomerom zahŕňajú:
- Leonardo Di Vinci - Mona Lisa, Vitruviánsky muž
- Botticelli - Zrodenie Venuše
- Michelangelo - Svätá rodina, 'David'
- Raphael - Ukrižovanie
- Rembrandt - Autoportrét
- Salvador Dalí - Sviatosť poslednej večere, vytrvalosť pamäti
Použitie zlatého rezu v umeleckej kompozícii
V rámci zlatého obdĺžnika sú určité oblasti, o ktorých sa zistilo, že sú vizuálne príťažlivejšie ako iné oblasti. Tieto body sa objavia nakreslením čiary zo spodného rohu obdĺžnika do opačného rohu a jej opakovaním s druhým spodným rohom. Tieto čiary sa budú pretínať v presnom strede Zlatého obdĺžnika. Ďalej zmerajte stred pozdĺž každej čiary začínajúc od stredového bodu. Tieto štyri body sa nazývajú oči obdĺžnika (zlatý pomer). Hlavné ohnisko maľby je potom nakreslené alebo namaľované v rámci týchto bodov záujmu (pomerov).
Zlatý pomer v hudbe

Hudba sa skladá z číselnej hodnoty a keď sa na vytvorenie hudobného diela použije zlatý pomer, stáva sa živým príkladom matematiky. Fibonacciho sekvencia prevláda aj v hudbe:
- Na stupnici je osem nôt.
- Tretia a piata nota sú základom akordov.
- Dĺžka alebo oktáva akejkoľvek noty je 13 nôt.
Sekvencia pokračuje v celej hudobnej skladbe a stáva sa zložitejšou, keď dosiahne Zlatý pomer.
Skladatelia, ktorí použili zlatý pomer
Niektorí z najznámejších klasických skladateľov používali vo svojich hudobných skladbách zlatý pomer a Fibonacciho sekvenovanie, vrátane Bacha, Beethovena, Chopina a Mozarta. Niektorí moderní skladatelia ako Casey Mongoven vo svojej hudbe preskúmali zlatý rez.
Príklady zlatého pomeru v prírode

Kde sa v prírode nachádza zlatý rez? Je v zlatej alebo Fibonacciho špirále, ktorú je možné vytvoriť pomocou zlatého pomeru. Toto je fenomén, ktorý sa vo veľkej miere vyskytuje v prírodnom svete. Listy rastliny rastú tak, aby ich čo najviac mohlo stúpať po stonke. Nový list sa vytvorí až po postupe, ktorý vytvoril.
- Špirálové kaktusy
- Špirálové galaxie
- Slnečnice
Kvety s Fibonacciho postupnosťou
Niektoré kvety majú okvetné lístky, ktoré nasledujú Fibonacciho postupnosť:
- Tri okvetné lístky:Kosatec, ľalia, orchidey, trillium
- Päť okvetných lístkov: Masláky, muškáty, ibišteky, svlačec, nasturtium
- Osem okvetných lístkov: Delphiniums
- 13 okvetných lístkov: Určité odrody sedmokrásky, ruža, nechtík
Fibonacciho špirála v šiškach

V závislosti od druhu drevín môžete zlatý rez vidieť aj v rámci Fibonacciho číselného radu v šiškach. Na jednej strane šišky nájdete sériu ôsmich špirál, na druhej strane 13 špirál. Ďalší vzor šišky má päť špirál na jednej strane a osem na druhej.
Zlatý pomer u ľudí
Tento pomer je dôležitý nielen pre to, ako sa ľudia navzájom pozerajú, ale aj pre to, ako fungujú ich telá a pre ich DNA.
DNA odhaľuje zlatý pomer
Jeden z najúžasnejších príkladov zlatého rezu sa nachádza v štruktúre ľudskej DNA. To je možné vidieť na jednom priereze DNA, ktorý odhaľuje, že dvojitá špirála DNA tvorí tvar desaťuholníka. Ide o kombináciu dvoch päťuholníkov, otočených od seba o 36 stupňov, tvoriacich dvojitú špirálu DNA. Samotná špirála s dvojitou špirálou tvorí päťuholník. Dokonca aj jedna molekula DNA odhaľuje základ Zlatého rezu alebo Božskej proporcie.
Matematika za zlatým rezom
Nájsť zlatý rez v reálnom živote je jednoduché, pretože sa objavuje všade okolo vás. Je to matematická pravda, ktorá sa používa na definovanie toho, čo je bežne známe ako dokonalé číslo nachádzajúce sa v prírode, ktoré ľudia po stáročia duplikovali a napodobňovali. Zjednodušujúca krása tohto čísla maskuje jeho zložitosť pri vykonávaní. Aby ste pochopili teóriu zlatého pomeru, musíte najprv preskúmať Fibonacciho radenie pomeru.
Fibonacciho postupnosť a zlatý pomer
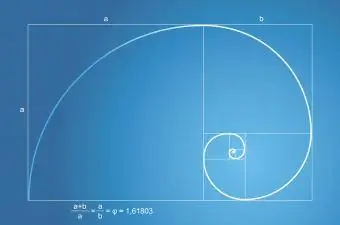
Fibonacciho postupnosť alebo séria má vzťah k zlatému rezu. Séria Fibonacci sa prejavuje v počte listov na rastline a počte okvetných lístkov na kvete. Fibonacciho špirála, ktorá sa nachádza v prírode, je vždy súčasťou zlatého obdĺžnika so zlatým pomerom.
Matematika Fibonacciho série je jednoduchá:
- Sekvencia začína 0 a 1.
- Stačí sčítať posledné dve čísla a získate ďalšie číslo v rade.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 atď.
- Tento príklad Fibonacciho radu vyzerá takto: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 atď.
Fibonacciho vzťah k Zlatému rezu sa realizuje, keď sa pridáva dopredu, ďalej a ďalej. Čím viac sérií pridávate, tým viac sa približujete k Zlatému rezu.
Vytvorenie zlatého obdĺžnika a trojuholníka
Ak chcete vytvoriť zlatý obdĺžnik s Fibonacciho postupnosťou, začnete štvorcom. Začnete stavať obdĺžnik pridaním ďalšieho štvorca k pôvodnému štvorcu. Nezabudnite použiť vzorec: 0+1=1 je prvý štvorec, 1+1=2 - pridáte ďalší štvorec.1+2=3 pridáte tri štvorce a potom, 2+3=5, pridáte päť štvorcov. Budete pokračovať v pridávaní štvorcov a nakoniec vytvoríte Zlatý obdĺžnik.
Zlatý trojuholník možno vytvoriť rozpoltením zlatého obdĺžnika z jedného rohu do opačného rohu. Toto vytvorí trojuholník, ktorého tri strany alebo uhly majú pomer 2:2:1, čo znamená, že dve dlhé strany majú rovnakú dĺžku a krátky uhol je presne polovica dĺžky dvoch dlhších.
Zlatý pomer v reálnom svete
Zlatý pomer je často označovaný ako božský pomer kvôli jeho dôležitosti v prírode a v ľudských telách. Zistenie, že zlatý rez je prítomný v toľkých živých veciach, podporilo úctu k tejto magickej proporcii a dodnes je inšpiráciou pre umelcov a tvorcov.






